New SE CASC Publication Provides an Extended Framework to Address Conservation Planning Problems

SE CASC Research Ecologist, Mitch Eaton, co-authored the paper, Spatial conservation planning under uncertainty using modern portfolio theory and Nash bargaining solution, which was recently published in the journal, Ecological Modelling. This publication derived from work on the SE CASC project, Climate Change Adaptation for Coastal National Wildlife Refuges.

Spatial Conservation Planning Under Uncertainty Using Modern Portfolio Theory and Nash Bargaining Solution

Alvaro Sierra-Altamiranda, Hadi Charkhgard, Mitchell Eaton, Julien Martin, Simeon Yurek, Bradley J.Udell
Journal Abstract

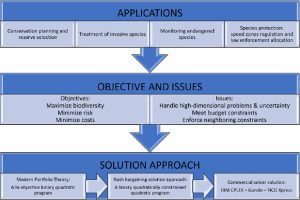
In recent years, researchers from interdisciplinary teams involving ecologists, economists and operations researchers collaborated to provide decision support tools to address the challenges of preserving biodiversity by optimizing the design of reserves. The goal of this paper is to further advance this area of research and provide new solutions to solve complex Spatial Conservation Planning (SCP) problems under uncertainty that consider risk preferences of decision makers. Our approach employs modern portfolio theory to address uncertainties in SCP problems, and involves two conflicting objectives: maximizing return and minimizing risk. We apply concepts from game theory such as the Nash bargaining solution to directly compute a desirable Pareto-optimal solution for the proposed bi-objective optimization formulation in natural resource management problems. We demonstrate with numerical examples that by directly computing a Nash bargaining solution, a Binary Quadratically Constrained Quadratic Program (BQCQP) can be solved. We show that our approach (implementable with commercial solvers such as CPLEX) can effectively solve the proposed BQCQP for much larger problems than previous approaches published in the ecological literature. Optimal solutions for problems with less than 400 parcels can be computed within a minute. Near optimal solutions (within at most 0.2% gap from an optimal solution) for high-dimensional problems involving up to 800 parcels can be computed within 8 h on a standard computer. We have presented a new approach to solve SCP optimization problems while considering uncertainty and risk tolerance of decision makers. Our new approach expands considerably the applicability of such SCP optimization methods to address real conservation problems.